gnuComet - Putting fun back to the early 90's !

When we flew without the current limitations, without a parachute, without a license, flying imaginative wings of bright colors, no money, no car, and we were young...! :)

Figure 1. gnuComet planform

1. DESCRIPTION

gnuComet is an attempt to recreate a simple and fun wing, as was done in the 90's. An attractive planform shape, few cells (28) and compact aspect ratio (4.27), many lines for a sense of passive safety and durability.
Steering harness 'sellette de pilotage' and PE 'pilotage exigeant' by default, and normal harness for PA 'pilotage aise' as optional. Don't worry, the use of the steering seat was not as unstable and difficult as has been said (PE).
On the contrary, it was a totally intuitive method of control and an indescribable feeling of softness. Let’s experiment again, or for the first time!

Size	M
Surface (m2)	25 m2
Flat span (m)	10.33
Flat AR	4.27
Cells	28
Closed cells	4+0,5+0,5
Weight range (Kg)	60-80
Glide ratio	5.9+
Anchors per rib	4
Risers	3 or 4
Extrados and intrados	ripstop 40 gr/m2
Ribs	ripstop 40 gr/m2 hard
Lines (m)	367 m
Normal risers	Yes
Vario seat	Yes
Certification	No

2. PLANS

Basic geometry: pre-data.txt geometry.dxf gnuComet-basicgeo.dxf

LEP files: leparagliding.txt gnua.txt lep-out.txt lines.txt

dxf files: leparagliding.dxf.zip lep-3d.dxf.zip

3. SCREENSHOTS

s6

4. THE STEERING SEAT

Three points steering seat. A geometric model.

Figure 2. Consider a three-point control harness. Risers A (red), B (green) and C (orange), are fixed to a seat with padded rigid plate at points 1,2 and 3. Riser A is fixed at point 1 '' with a spacer up to point 2 '' where riser B slides freely, and another spacer up to point 3 '' where riser C slides freely.

We can consider a first simplified model where point 1 is fixed, and the plate rotates an alpha angle with respect to this point. Tilting our weight forward, the plate rotates a positive angle. Point 2 moves to position 2 ', and riser B slides up through point 2' '. Point 3 moves to position 3 ', and riser C slides up through point 3' '. The result is wing acceleration. By tilting the weight backwards, the alpha angle is negative, and the result is the slowing of the wing.

This way we can adjust the angle of incidence of the wing dynamically and intuitively. The control is complemented by moving the weight of our body to the side where we want to turn. Thus additional control with the commands is less necessary.

Now let's calculate what is the elongation or shortening caused on the risers by an alpha angle on the rigid plate.

If we look at the detail drawing at the bottom right, point 2 moves to a 2 'position. Considering orthogonal axes centered at point 1, and s2 the separation between points 1 and 2, the coordinates of point 2 'are:
2'x = s2 · con (alpha)
2'y = s2 · sin (alpha)

The distance between points 2 'and 2' 'is calculated by its coordinates, which are known:
dist(2'-2'')=sqrt((2'x-2''x)^2+(2'y-2''y)^2)
And the same to calculate the distance between points 2 and 2'':
dist(2-2'')=sqrt((2x-2''x)^2+(2y-2''y)^2)

The experimental elongation for riser B is:
dist (2-2 '') - dist (2'-2 '')

And the lengthening of riser C calculated in the same way:
dist(3-3'')-dist(3'-3'')

Now, we have a good mathematical approximation of how the lengths of the risers vary, depending on the geometry of the steering seat.

The next step will be study other possible configurations of the position of the plate and risers assembly, and study the need to add diagonal lines to limit extreme plate positions, if necessary.

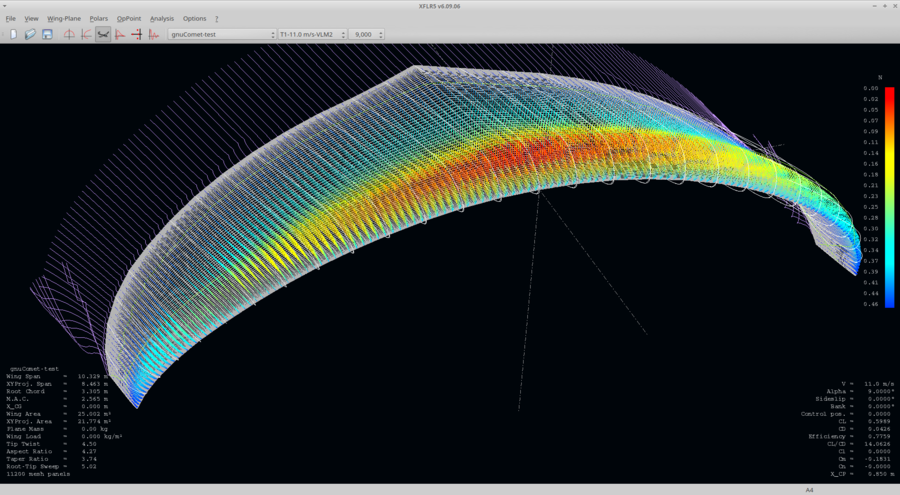
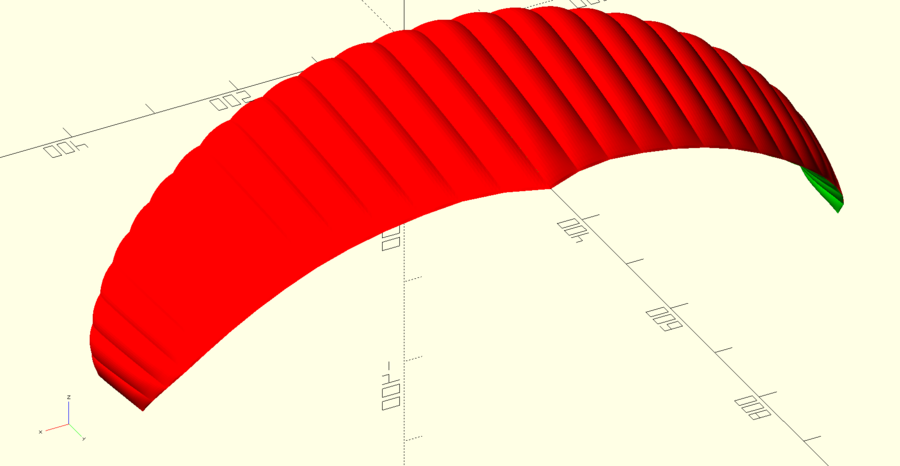
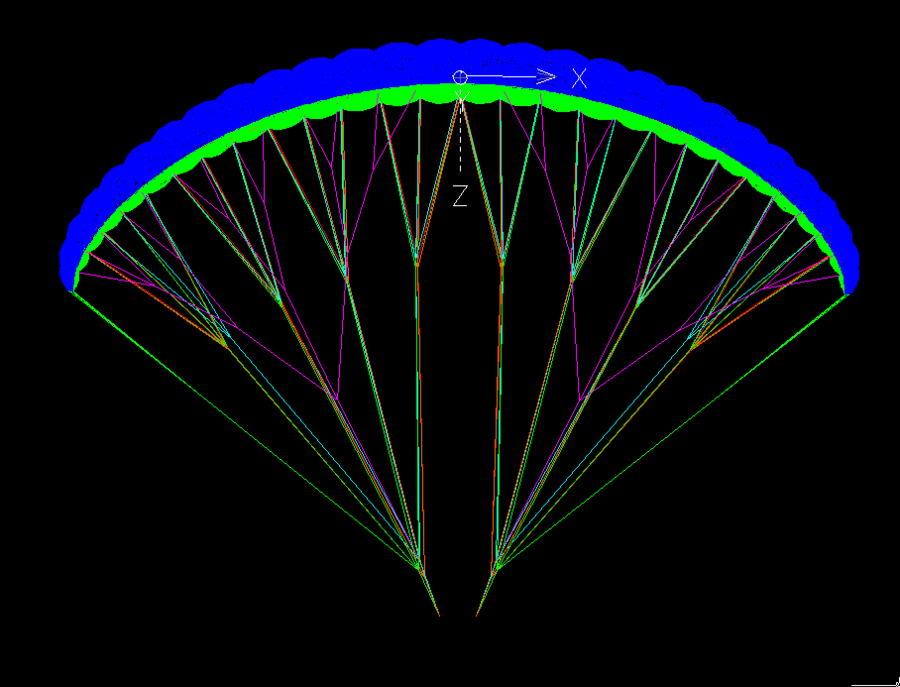
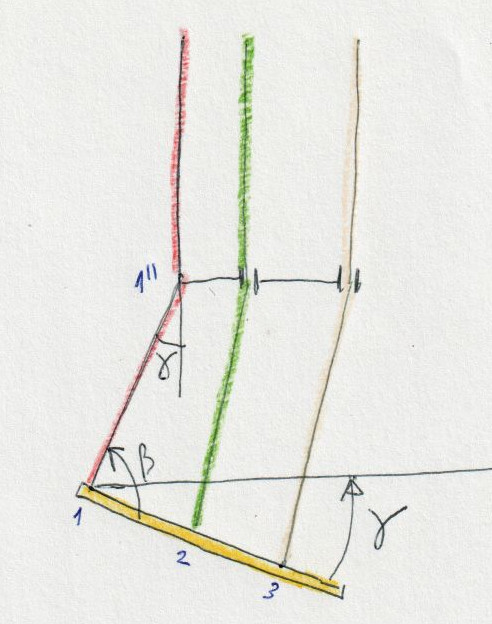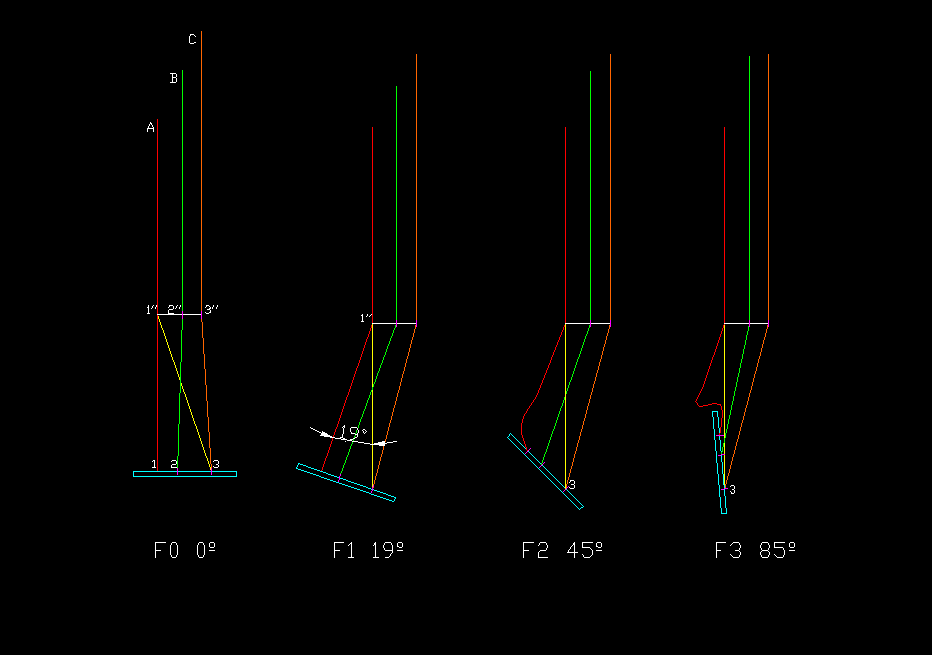
Figure 3. The steering seat can take other geometric forms in flight. We consider a model where the strap 1-1 '' turns a gamma angle at point 1 '' with respect to the vertical, and the seat plate is still perpendicular to the strap 1-1 ''.

We see that this is approximately equivalent to rotate the seat plate an angle -Alpha in the previous model. That is, if we turn a gamma angle we get a lower speed, and if at the same time we apply an angle -Alpha, we accelerate. Combining Angles Gamma and Alpha we get different configurations. Generally, Gammma angle will be small, and we consider Alpha angle as more representative of the model.

Figure 4. Let's consider an extreme situation in the plate position. In drawing I) the plate is in a slow and almost vertical position.
The maximum shortening in riser B is s2, and the maximum shortening in riser C is s3. We can define the lengths s2 and s3, so that in the extreme case of plate in maximum slow position or fast plate, the paraglider has permissible flight speeds. In the maximum speed position, there is the possibility of frontal collapse, and in the minimum speed position there is the possibility of entering a stall.

We can add a strap to limit some of the positions. For example, we can add a diagonal strap joining points 1'' and 3 (drawing II). If length 1''-3 is less than the sum of lengths 1''-1 and s3, this strap will modify the maximum shortening of risers B and C. In the extreme position of drawing III) the result is that the plate approaches point 1'' vertically by a length which is the remainder between (1-1'' + s3) and the length d. This vertical rise is the reduction (red) in length experienced by the 1-1'' strap. In extreme slow position riser B is shortened by a distance s2-red, and riser C by a distance s3-red.

Vario seat real measures and graphical experiment

First, let's define the measures of a classical three points vario seat:

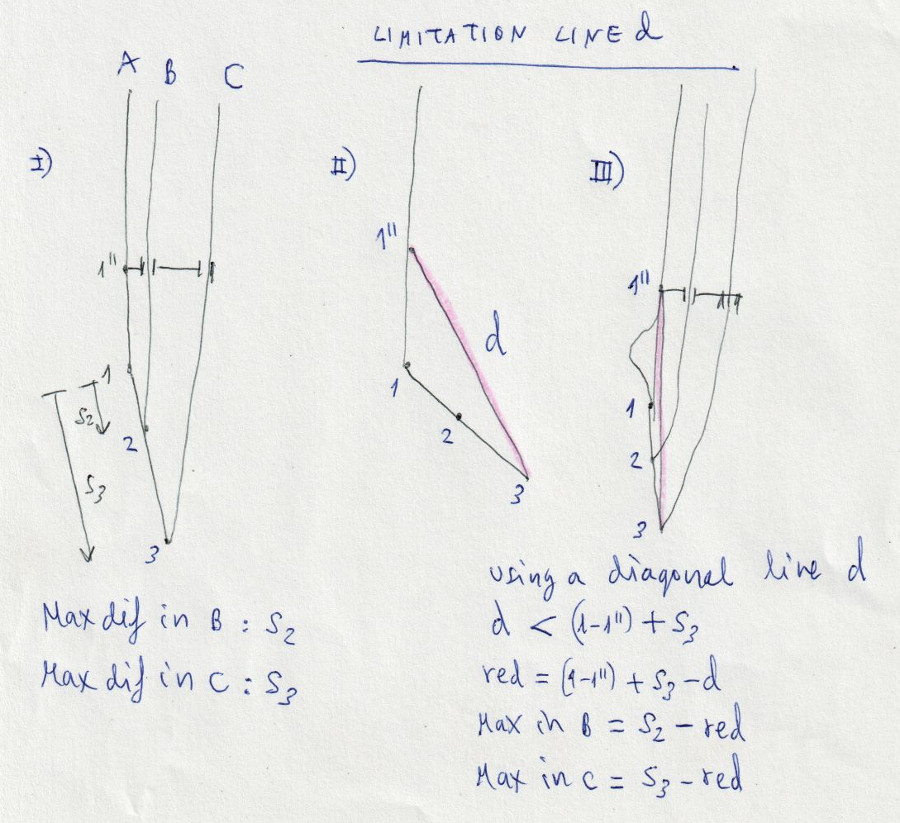
A	72	cm	A riser
B	82	cm	B riser
C	90	cm	C riser
1-1’’	32	cm
s2	4	cm
s3	11	cm
r2	5	cm
r3	9	cm
1’’-3	33,8	cm
d	34	cm	Diagonal strap

Now we can draw the basic lines of the harness, and see what happens when we apply different angles to the seat plate:

vs-1

Figure 5. Vario seat positions between -85 and 85 degrees

By applying a clockwise rotation to the plate around point 1, the effect is that risers B and C are progressively shortened. For example in position P3 at 85º (almost vertical) B is shortened by 4.3 cm and C by 11.6 cm. This slows the wing down a lot, maybe too much and it can go into aerodynamic loss. Applying a counter-clockwise rotation of 85º, the effect is that B lengthens by 3.6 cm and C lengthens by 9.5 cm. This is very similar to pressing the pedal of the speed system, but much more comfortable, just shifting the weight forward.

vs-2

Figure 6. Vario seat using diagonal limitation strap 1''-3 (yellow line)

A recommended improvement is to limit the maximum rearward position to prevent the wing from stalling. The solution is to add an strap between points 1'' and 3. Let's see how this works:
At the 0º position, the 1''-3 line (yellow) is not working. By moving the weight back slightly, we can reach the position where the diagonal line 1''-3 is vertical, and the riser A is still perpendicular to the plate. In this case the rotation angle is 19º. Throughout this range, the system operates linearly, similar to the system in Figure 5. We can measure in the drawing that in position F1, riser B is shortened by 1.6 cm and riser C by 2.9 cm. From position F1, and moving the weight further back, the plate begins to rotate at point 3, and an interesting phenomenon occurs: the riser B begins to lengthen, and C remains almost constant. So in extreme position F4 (almost vertical plate), riser B is lengthened (in relation to A) by 4.6 cm, and C is shortened by 2.9 cm. Thus the maximum backward position is limited. And the extension of riser B creates a small concavity in the profile, i.e. it increases the wing lift, ideal for taking advantage of small thermal or dynamic ascents. This is the theory of the vario seat, accelerate fast and effortless when necessary and slow down and improve the profile to take advantage of the smallest ascents. All this in an intuitive and instantaneous way. Of course we add the good directional control achieved by shifting the weight of our body to one side or the other.

View here the spreadsheet (.ods) with the elongation and shortening values obtained in the different drawings, here in DXF.

Other projects (back to 1988!):

gnu922 (9x2 cells year 2022)
gnu1122 (11x2 cells year 2022)