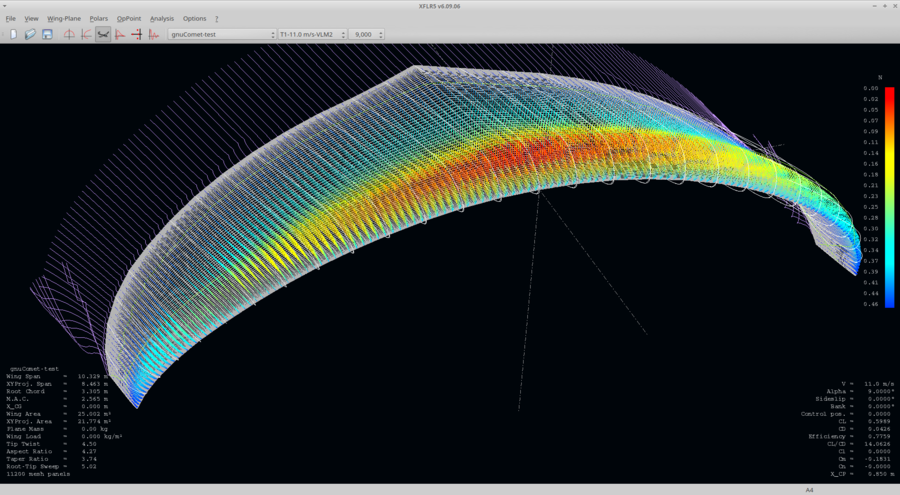
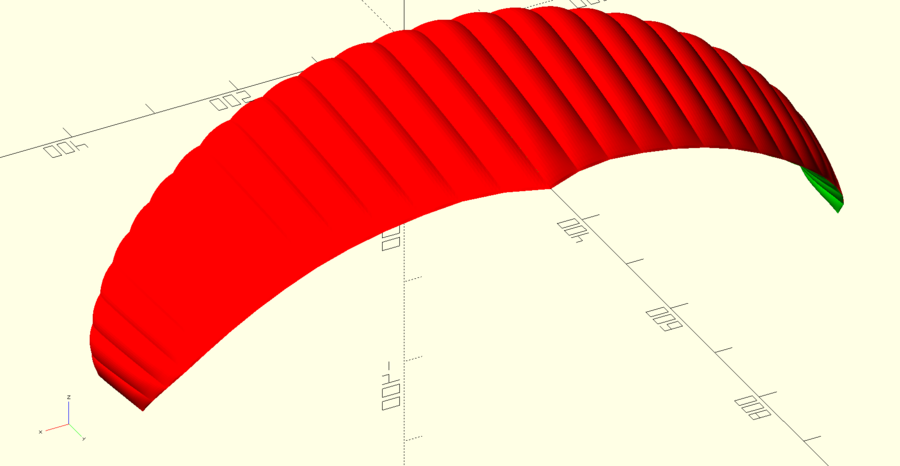
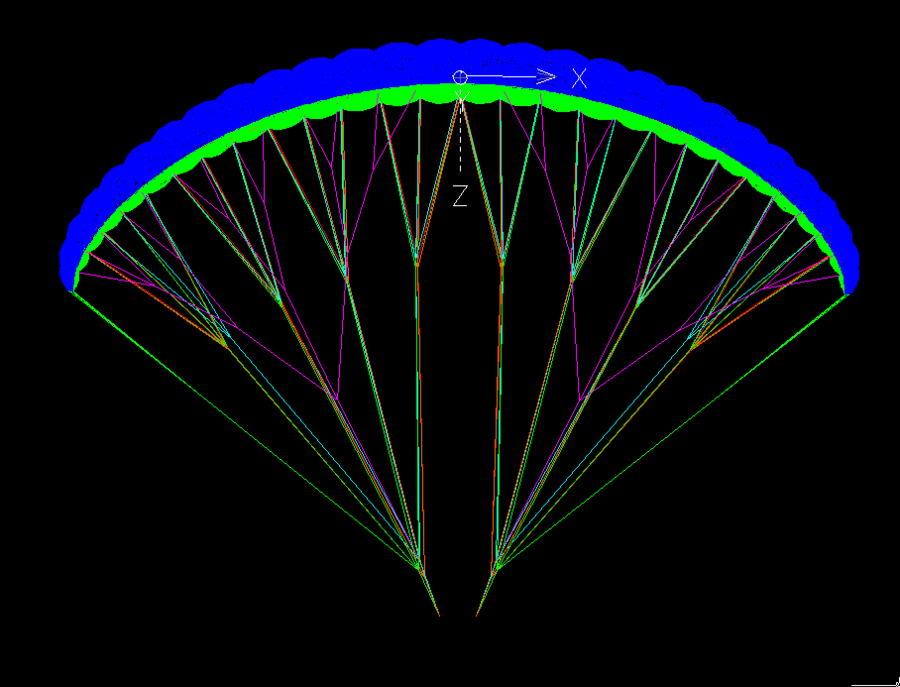
gnuComet - Remettre le vol plaisir au début des années 90's !

Quand on volait sans les limitations actuelles, sans parachute, sans permis de vol, avec des ailes innovantes aux couleurs vives, sans argent, sans voiture, et nous étions jeunes...! :)

Figure 1. gnuComet planform

1. DESCRIPTIF

gnuComet est une tentative de recréer une aile simple et amusante, comme cela se faisait dans les années 90. Une forme en plan attrayante, peu de cellules (28) et un allongement compact (4.27),
de nombreuses lignes pour un sentiment de sécurité passive et de durabilité. Harnais avec 'sellette de pilotage' et PE 'pilotage exigeant' par défaut, et harnais normal pour PA 'pilotage aise' en option.
Rassurez-vous, l'utilisation de la sellette de pilotage n'était pas aussi instable et difficile qu'on l'a dit (PE).
Au contraire, c'était une méthode de contrôle totalement intuitive et une sensation de douceur indescriptible. Expérimentons à nouveau, ou pour la première fois !

Taille	M
Surface (m2)	25 m2
Envergure (m)	10.33
Allongement	4.1
Caissons	28
Caissons fermés	4+0,5+0,5
Plage de poids (Kg)	60-80
Finesse	5.9+
Ancrages	4
Élévateurs	3 / 4
Extrados and intrados	ripstop 40 gr/m2
Ribs	ripstop 40 gr/m2 hard
Lignes (m)	-
Élévateurs normals	Oui
Sellette de pilotage	Oui
Certification	Non

2. PLANS

Géométrie de base: pre-data.txt geometry.dxf gnuComet-basicgeo.dxf

LEP fichiers: leparagliding.txt gnua.txt lep-out.txt lines.txt

dxf fichiers: leparagliding.dxf.zip lep-3d.dxf.zip

3. SCREENSHOTS

s6

4. ÉTUDE D'ÉQUILIBRE

Etude d'équilibre par François de Villiers, avril 2024.

pdf document

Etude d'équilibre par François de Villiers, avril 2024.
fichiers txt d'entrée et de sortie, résultats des cas AoA 4 et 5,9 degrés comet7z

5. LA SELLETTE DE PILOTAGE

Sellette de pilotage trois points. Un modèle géométrique.

Figure 2. Considérez une sellette à trois points. Les élévateurs A (rouge), B (vert) et C (orange), sont fixés sur un siège avec plaque rigide rembourrée aux points 1,2 et 3. L'élévateur A est fixé au point 1'' avec une entretoise jusqu'au point 2' ' où l'élévateur B coulisse librement, et une autre entretoise jusqu'au point 3 '' où l'élévateur C coulisse librement.

On peut considérer un premier modèle simplifié où le point 1 est fixe, et la plaque tourne d'un angle alpha par rapport à ce point. Inclinant notre poids vers l'avant, la plaque tourne d'un angle positif. Le point 2 se déplace en position 2', et l'élévateur B glisse par 2''. Le point 3 se déplace en position 3', et l'élévateur C glisse par le point 3''. Le résultat est une accélération de l'aile. En inclinant le poids vers l'arrière, l'angle alpha est négatif, et le résultat est le ralentissement de l'aile.

De cette façon, nous pouvons ajuster l'angle d'incidence de l'aile de manière dynamique et intuitive. Le contrôle est complété par le déplacement du poids de notre corps du côté où nous voulons tourner. Ainsi, un contrôle supplémentaire avec les commandes est moins nécessaire.

Calculons maintenant quel est l'allongement ou le raccourcissement causé sur les élévateurs par un angle alpha sur la plaque rigide.

Si on regarde le dessin de détail en bas à droite, le point 2 se déplace vers une position 2'. En considérant des axes orthogonaux centrés au point 1, et s2 la séparation entre les points 1 et 2, les coordonnées du point 2' sont :
2'x = s2 · con (alpha)
2'y = s2 · sin (alpha)

La distance entre les points 2' et 2'' est calculée par ses coordonnées, qui sont connues :
dist(2'-2'')=sqrt((2'x-2''x)^2+(2'y-2''y)^2)
Et pareil pour calculer la distance entre les points 2 et 2'' :
dist(2-2'')=sqrt((2x-2''x)^2+(2y-2''y)^2)

L'allongement expérimenté pour l'élévateur B est :
distance (2-2 '') - distance (2'-2 '')

Et l'allongement de l'élévateur C calculé de la même façon :
dist(3-3'')-dist(3'-3'')

Maintenant, nous avons une bonne approximation mathématique de la façon dont les longueurs des élévateurs varient, en fonction de la géométrie de la sellette de pilotage.

La prochaine étape sera d'étudier d'autres configurations possibles de la position de l'ensemble plaque et éleévateurs, et d'étudier la nécessité d'ajouter des lignes diagonales pour limiter les positions extrêmes de la plaque, si nécessaire.

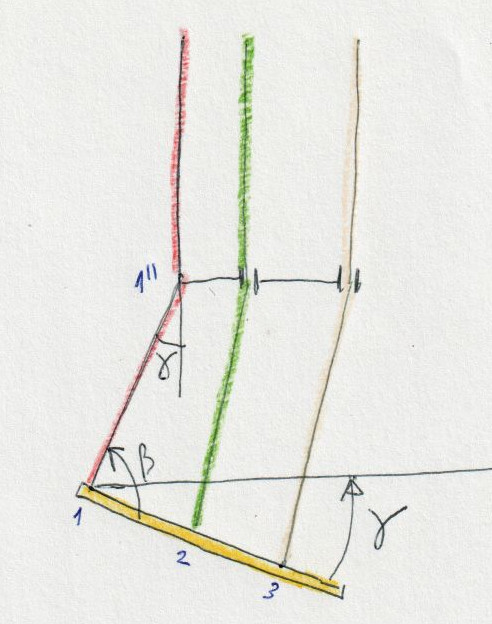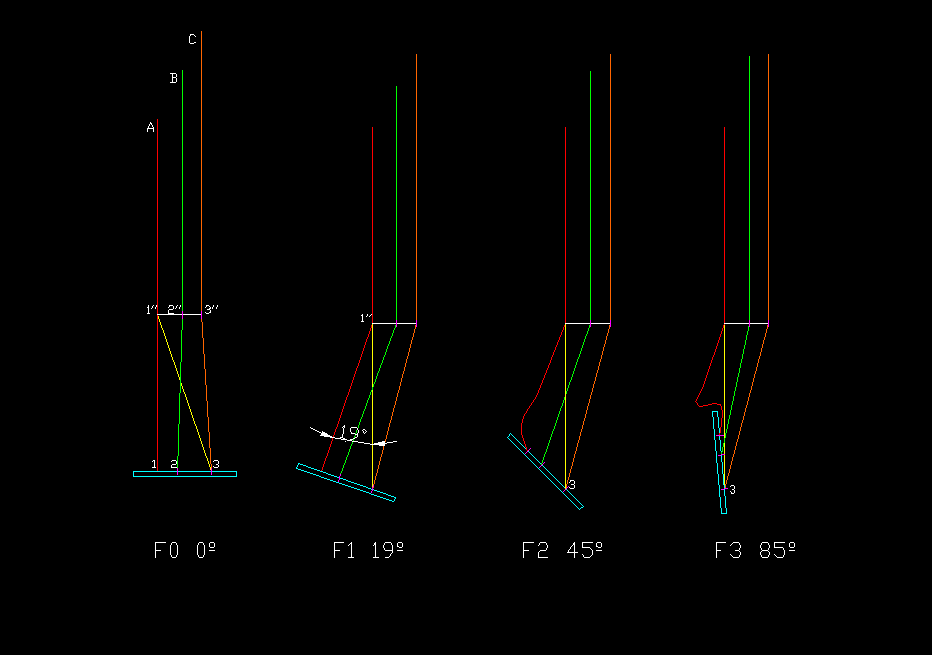
Figure 3. Le sellette de pilotage en vol peut prendre d'autres formes géométriques. Nous envisageons un modèle où la sangle 1-1'' tourne un angle gamma en 1'' par rapport à la verticale, et la plaque de la sellette est toujours perpendiculaire à la sangle 1-1''.

Nous pouvons voir que cela équivaut à peu près à tourner la plaque de la sellette un angle -alpha sur le modèle précédent. Autrement dit, si nous faisons pivoter l'angle gamma, nous obtenons moins de vitesse, et si nous appliquons l'angle -alpha en même temps, nous accélérons. En combinant les angles Gamma et Alpha, on obtient différentes configurations. En règle générale, l'angle Gamma sera petit et nous considérons que l'angle Alpha est plus représentatif du modèle.

Figure 4. Considérons une situation extrême dans la position de la plaque. Dans le dessin I) la plaque est dans une position lente et presque verticale.
Le raccourcissement maximum dans le riser B est s2, et le raccourcissement maximum dans le riser C est s3. On peut définir les longueurs s2 et s3, de sorte que dans le cas extrême de plaque en position lente maximale ou de plaque rapide, le parapente ait des vitesses de vol admissibles. En position de vitesse maximale, il y a possibilité de fermeture frontale et en position de vitesse minimale, il y a possibilité d'entrer dans un décrochage.

On peut ajouter une sangle pour limiter certaines positions. Par exemple, on peut ajouter une sangle diagonale joignant les points 1'' et 3 (dessin II). Si la longueur 1''-3 est inférieure à la somme des longueurs 1''-1 et s3, cette sangle modifiera le raccourcissement maximum des élévateurs B et C. Dans la position extrême du dessin III) il en résulte que la plaque se rapproche point 1'' verticalement par une longueur qui est le reste entre (1-1'' + s3) et la longueur d. Cette montée verticale est la réduction (red) de longueur subie par la sangle 1-1''. En position extrême lente, la colonne montante B est raccourcie d'une distance s2-red, et la colonne montante C d'une distance s3-red.

Mesures réelles de la settette de pilotage et expérimentation graphique

Définissons tout d'abord les mesures d'un siège vario trois points classique :

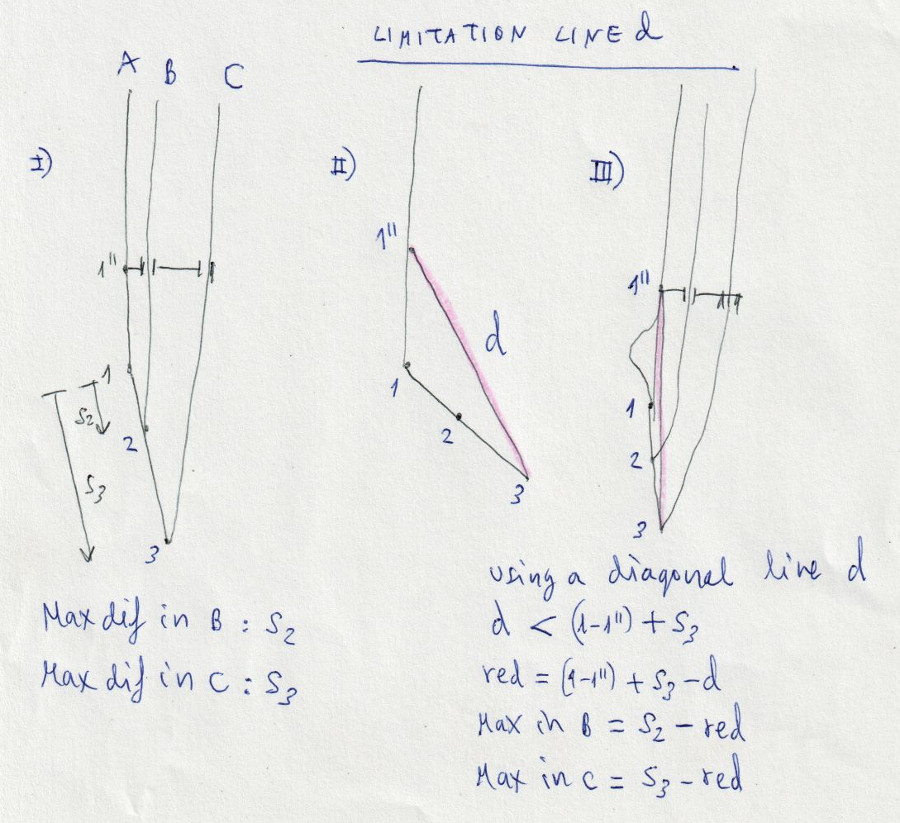
A	72	cm	A riser
B	82	cm	B riser
C	90	cm	C riser
1-1’’	32	cm
s2	4	cm
s3	11	cm
r2	5	cm
r3	9	cm
1’’-3	33,8	cm
d	34	cm	Diagonal strap

Nous pouvons maintenant tracer les lignes de base du harnais et voir ce qui se passe lorsque nous appliquons différents angles à la plaque sellette:

vs-1

Figure 5. Positions sellette pilotage entre -85 et 85 degrés

En appliquant une rotation dans le sens des aiguilles d'une montre à la plaque autour du point 1, l'effet est que les élévateurs B et C sont progressivement raccourcies. Par exemple en position P3 à 85º (presque verticale) B est raccourci de 4,3 cm et C de 11,6 cm. Cela ralentit beaucoup l'aile, peut-être trop et cela peut entraîner une perte aérodynamique. En appliquant une rotation anti-horaire de 85º, l'effet est que B s'allonge de 3,6 cm et C s'allonge de 9,5 cm. C'est très similaire à appuyer sur la pédale du système de vitesse, mais beaucoup plus confortable, en déplaçant simplement le poids vers l'avant.

vs-2

Figure 6. Sellette pilotage utilisant la sangle de limitation diagonale 1''-3 (ligne jaune)

Une amélioration recommandée est de limiter la position maximale vers l'arrière pour empêcher l'aile de décrocher. La solution est d'ajouter une sangle entre les points 1'' et 3. Voyons comment cela fonctionne :

A la position 0º, la ligne 1''-3 (jaune) ne fonctionne pas. En reculant légèrement le poids, on peut atteindre la position où la ligne diagonale 1''-3 est verticale, et l'élévateur A est toujours perpendiculaire à la plaque d'assise. Dans ce cas, l'angle de rotation est de 19º. Dans toute cette plage, le système fonctionne de manière linéaire, similaire au système de la figure 5. On peut mesurer sur le dessin qu'en position F1, l'élévateur B est raccourcie de 1,6 cm et l'élévateur C de 2,9 cm. A partir de la position F1, et en reculant le poids, le plate commence à tourner au point 3, et un phénomène intéressant se produit : l'élévateur B commence à s'allonger, et C reste quasiment constant. Ainsi en position extrême F4 (plaque presque verticale), l'élévateur B est allongée (par rapport à A) de 4,6 cm, et C est raccourcie de 2,9 cm. Ainsi, la position arrière maximale est limitée. Et le prolongement de l'élévateur B crée une petite concavité dans le profil, c'est à dire qu'il augmente la portance de l'aile, idéal pour profiter des petites ascendantes thermiques ou dynamiques. C'est la théorie du siège vario, accélérer vite et sans effort quand c'est nécessaire et ralentir et améliorer le profil pour profiter des plus petites ascendantes. Tout cela de manière intuitive et instantanée. Bien sûr, nous ajoutons le bon contrôle directionnel obtenu en déplaçant le poids de notre corps d'un côté ou de l'autre.

Visualisez ici la feuille de calcul (.ods) avec les valeurs d'allongement et de raccourcissement obtenues dans les différents dessins, ici en DXF.

Autres projets (retour à 1988 !) :

gnu922 (9x2 cellules année 2022)
gnu1122 (11x2 cellules année 2022)