3D Shaping

PART 1: NOTES ON 3D FORMATION OF THE LEADING EDGE IN A PARAGLIDER, USING RIPSTOP FABRICo

PART 1: Notes on the 3D formation of the leading edge in a paraglider, using ripstop fabric.
PART 2: 3D-SHAPING PROGRAMMING ESTRATEGY
PART 3: Negative 3D-shaping
PART 4: A device for experimental study of deformations and wrinkles

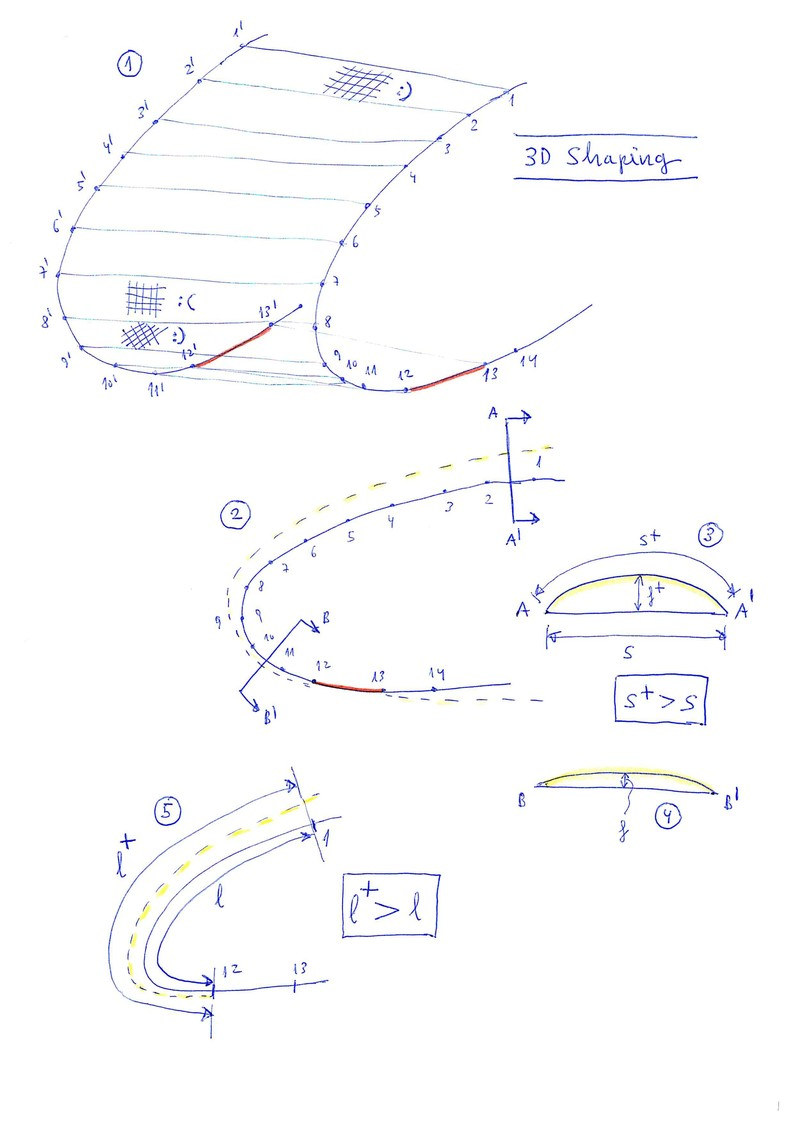
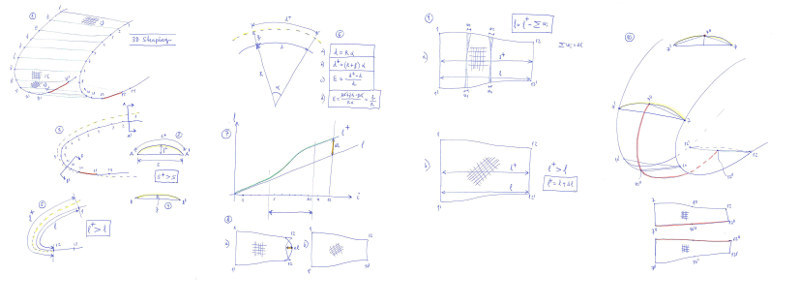
1. Leading edge model

Consider the frontal part (nose) of a cell formed between two consecutive profiles. The model considers the left profile, composed by successive points 1,2,3,4,... linked by segments. And the right profile, consisting of corresponding points 1',2',3',4'... The surface of the nose is formed through the space quadrilateral 1-1'-2-2', and successives.

2. Ovalization

Consider a side view of the nose. Considering that the internal pressure of the wing is greater than the external, the cell adopts a cylindrical shape (ovalization). At the front of the wing, it is advisable to increase the tension of the fabric forcing less ovalization. The approximate profile of ovalization is marked in dashed yellow line.

3. 4. Sections

Sections 3 and 4 showing a section of the panel in two different points. It shows the first problem to solve in the formation of the 3D surface. The distance along the fabric (s+) is greater than the straight-line distance between corresponding points (s). This is easily solved by adding a little of fabric laterally.

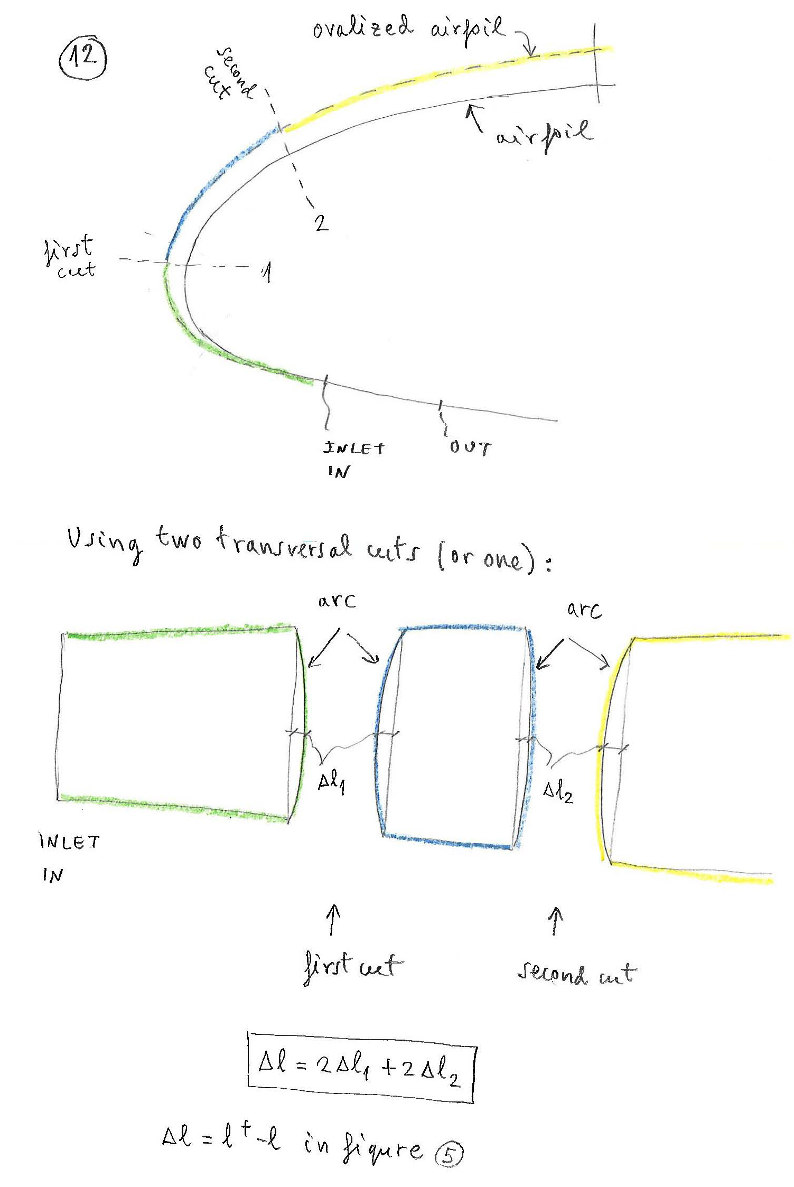
5. Length differences in the nose panel

If we look from the side view, we see the second problem. The length (l+) along the center of the ovalized panel (ovalitzat) is greater than the lateral length (l).

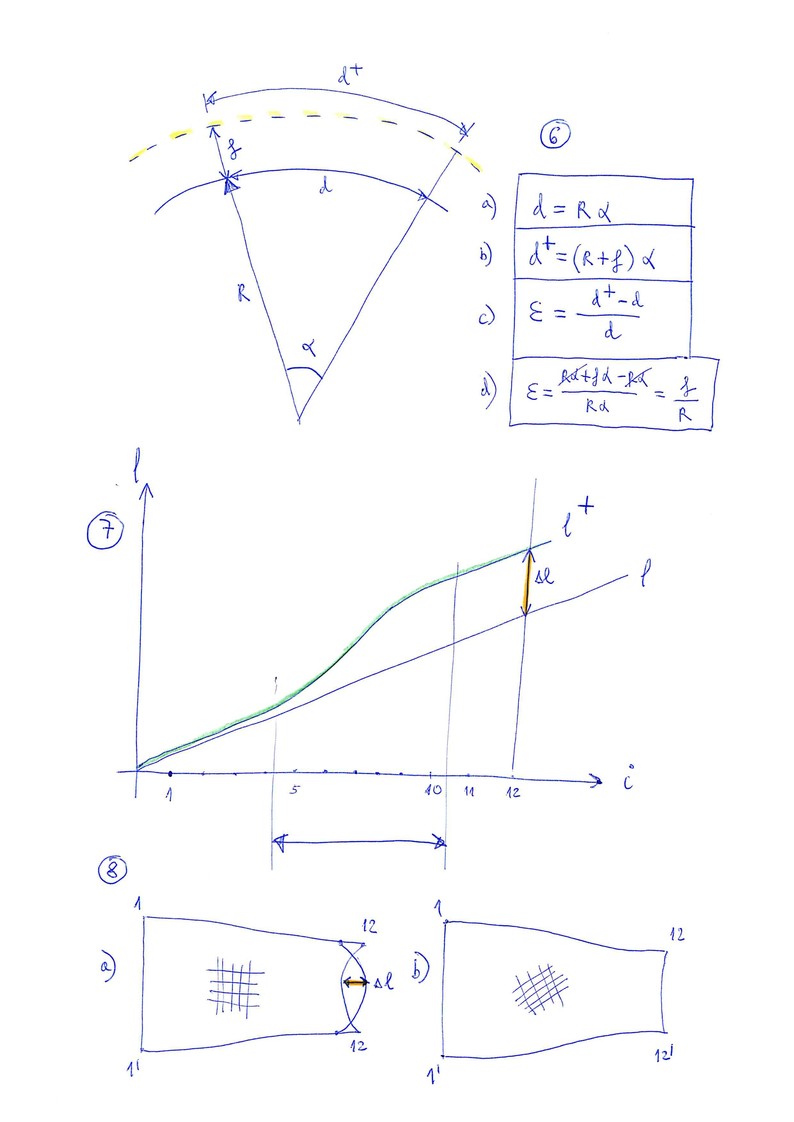
6. Deformation per unit

We deduce that the deformation per unit (epsilon) is directly proportional to the "arrow" (f) of the ovalization and inversely proportional to the radius (R) of curvature of the nose: Epsilon=f/R

7. Increments in length along nose

If we represent the accumulated length from the initial point of reference, we see a graph similar to the one represented. In the area of greatest curvature, is where the largest deformation will occur.

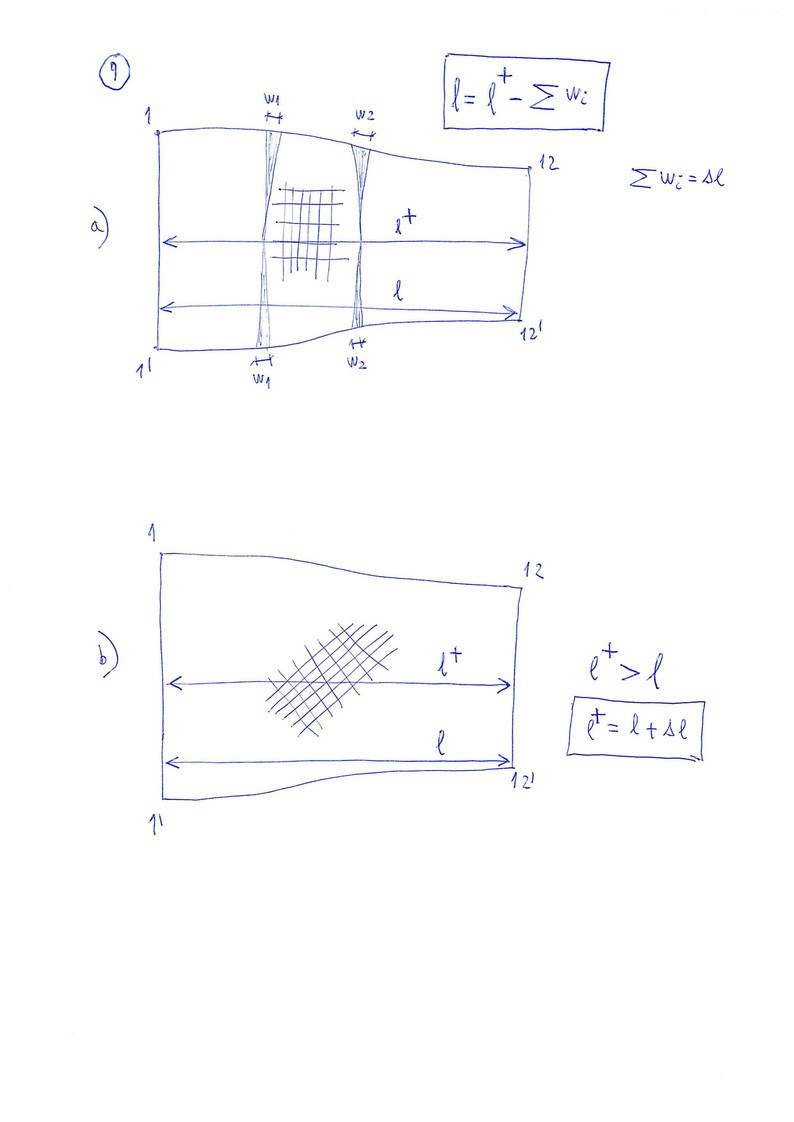
8. Problems in the panel

But the flat panel of ripstop fabric is not very deformable in the direction of the grid. So there will be problems in the final form (a figure).
Turning the grid of the panel 45 degrees, then the deformation required will be better adapted to the panel (b figure.

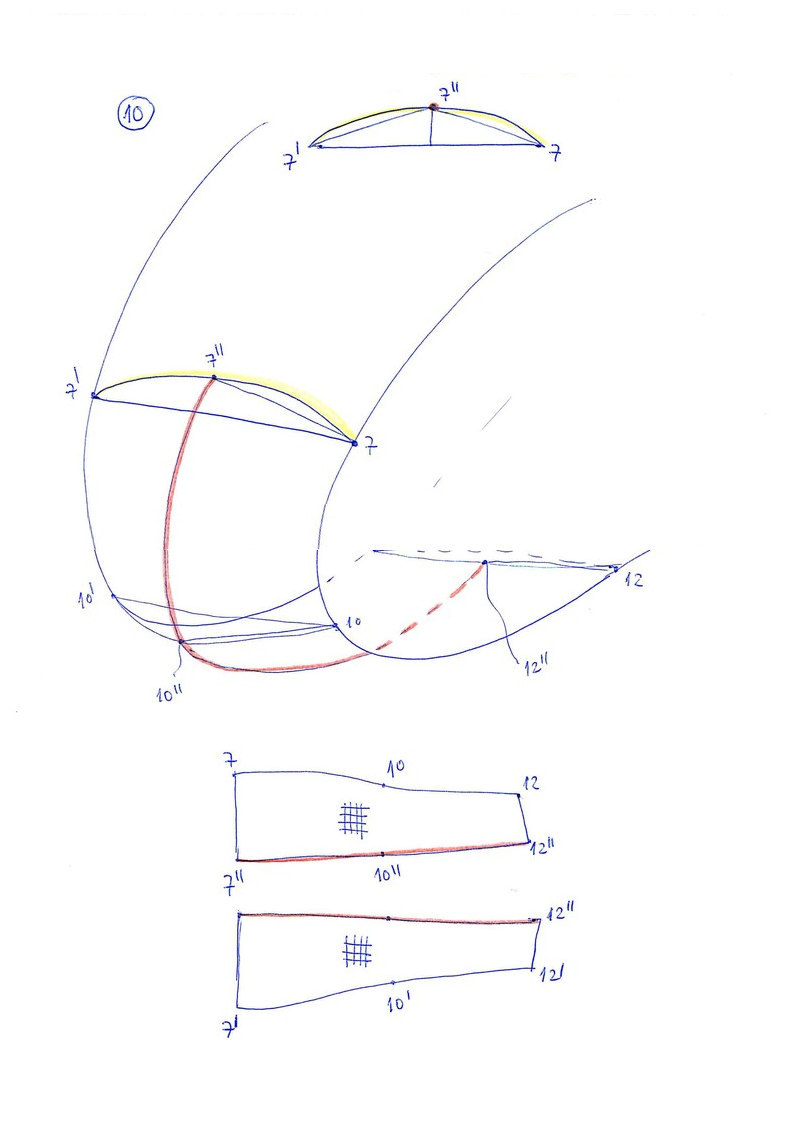
9. Details in the nose panel

Let's see in more detail. In the first case (a), since in the direction of the grid there is little distortion, the length of the panel reduces in lateral sides, forming small wrinkles (w). In the second case (b), the fabric is deformed in the center better to the required length. Naturally, to achieve this it is necessary to sew the nose panel with a separate piece of fabric, and properly oriented grid.

10. Other options

There are several possibilities to solve the second problem of 3D-shapping (9a), (9b), or the proposal in the figure 10. In this case, it is necessary to calculate a special line 7'', 8'', 9''... with a length (l+) of figure 5, and decompose the nose panel in two small panels, as shown in Figure 10. More difficult to calculate and sew, but possible.

11. Other. This option, used by some manufacturers, uses three pieces of fabric

Using tree pieces of fabric. The basic idea is to allow ovalization using a development with almost flat panels.

3D-Shaping in one image:

More graphical and numerical experiments soon. A graphical experiment is a drawing.
Even handmade, we can zoom in and explore interesting details. We have a lot of zoom!
We will do more graphical experiments, by hand and by computer.

12. 3D-Shaping using several tranversal cuts
Graphic experiment, added August 2018

This option is obvious and simple to sew. What is the goal of 3D-shaping? Simply adapt the fabric to the curved surfaces in two directions, so that the fabric works with a uniform tension. And that is useful? We need to make more graphical and practical experiments to decide. Look closely at Figure 12.

In the areas of profile that are almost straight (little curvature), the ovalized surface is a cylinder, which is developable in plan. In the areas of great curvature (nose) there is the problem that the panel is longer in the center than in the edges. We need more fabric in the center. A solution is to cut the panel transversely and progressively add tissue to the central zone by means of an arc. The arc will be equal to each side of the cut to allow a coincident seam. With one, two, or three cuts, we can get a very exact surface. Of course it is always an approach.

Calculation algorithm:
Define the zone where we apply the 3D.
Calculate increment of length (Dl) along the center of the panel, due to ovalization.
Define one or more cutting points 1,2,3...
Distribute the length increase (Dl) between the cutting points Dl1,Dl2,Dl3..., proportionally to the local curvature.
Draw the corresponding arcs in the resulting panels.