GNU sailwing

Эта глава описывает математический метод построения плоских панелей верхней и нижней поверхности секций.

Некоторые конструкторы используют 3D редакторы, такие как Rhino, 3Dstudiomax, но Лаборатией разработан небольшой простой алгоритм, делающий то же самое и получающий профили напрямую из 3D CAD программ.

5.2 Описание LE метода

1. Исходные данные - 3D модель параплана с профилями в тех местах, где они должны находиться.

2. Далее берем два соседних профиля, обозначаемых далеее профиль L (left) и профиль R (right).

3. Каждый профиль разделяем на две кривые (две 3D CAD полилинии), сответствующих верхней поверхности (между LE и TE) и нижней (между LE и TE). Воздухозаборники не входят в эти линии.

upper and lower surfaces
Рис 1: Верхняя и нижняя полилиния профиля

4. Берем полилинии от верхней панели между левым и правым профилем, каждый из которых состоит из равного количества N точек, где N достаточно большое число. Это точки из описания геометрии профиля. Можно запустить CAD комманду "_list " на полилинии, чтобы получить x, y, z координаты каждой из N точек. После чего копируем их в текстовый файл для последующей обработки нашей программой.

5. Основная идея заключается в том, что мы берем две соседние точки на левом профиле L1, L2 и на правом R1, R2, формирующих совместно параллелограмм. Теперь если мы разделим его диагональной линией, то получим два треугольника. Этот процесс называется триангуляцией. Мы можем найти стороны треугольников, потому что мы знаем координаты их вершин. Все что требуется, чтобы создать плоскую панель для любой изогнутой в пространстве поверхности, это поместить эти два треугольника на плоскость так, чтобы они соприкасались друг с другом своими "диагоналями" (сторонами, которые были раньше диагональю параллелограмма). Ошибка такого метода получения развертки минимальна, так как количество точек в профилях достаточно большое и каждый трегольник в отдельности является практически плоским.

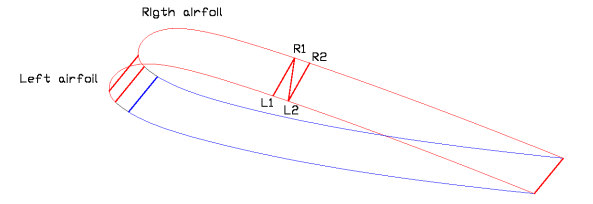
R-L airfoils
Рис. 2: Два соседний профиля и точки на них.

6. Дальше повторяем этот процесс для следующих точек: L2 и L3, R2 и R3, и так далее по всей поверхности. Результатом будет плоская поверхность, образованная треугольниками с совмещенными сторонами.

flat panel
Рис. 3: Плоская панель

7. Далее необходимо повторить процесс (4) для L и R полилиний для нижней поверхности.

8. И последнее, необходимо повторить начиная с пункта (2) для всех соседних профилей в половине крыла (так как вторая половина является симметричной, то ее можно не обрабатывать).