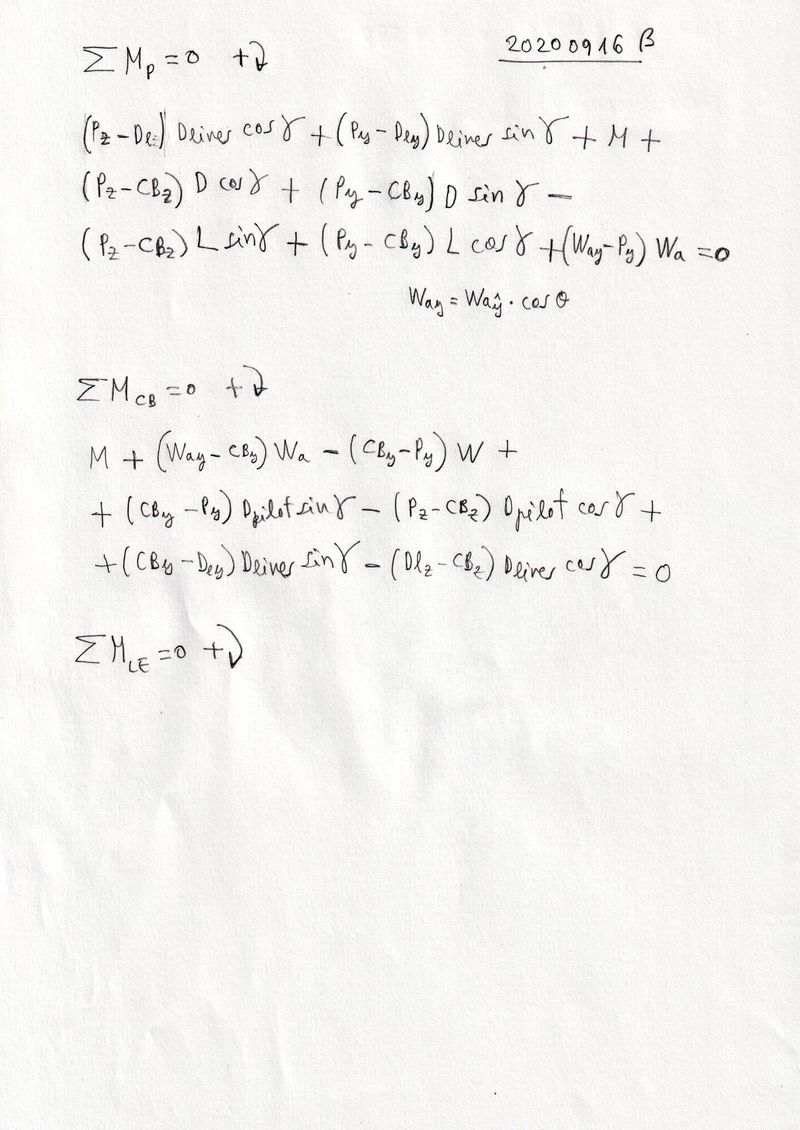PARAGLIDER EQUILIBRIUM
September 2020, thinking again about equilibrium...:
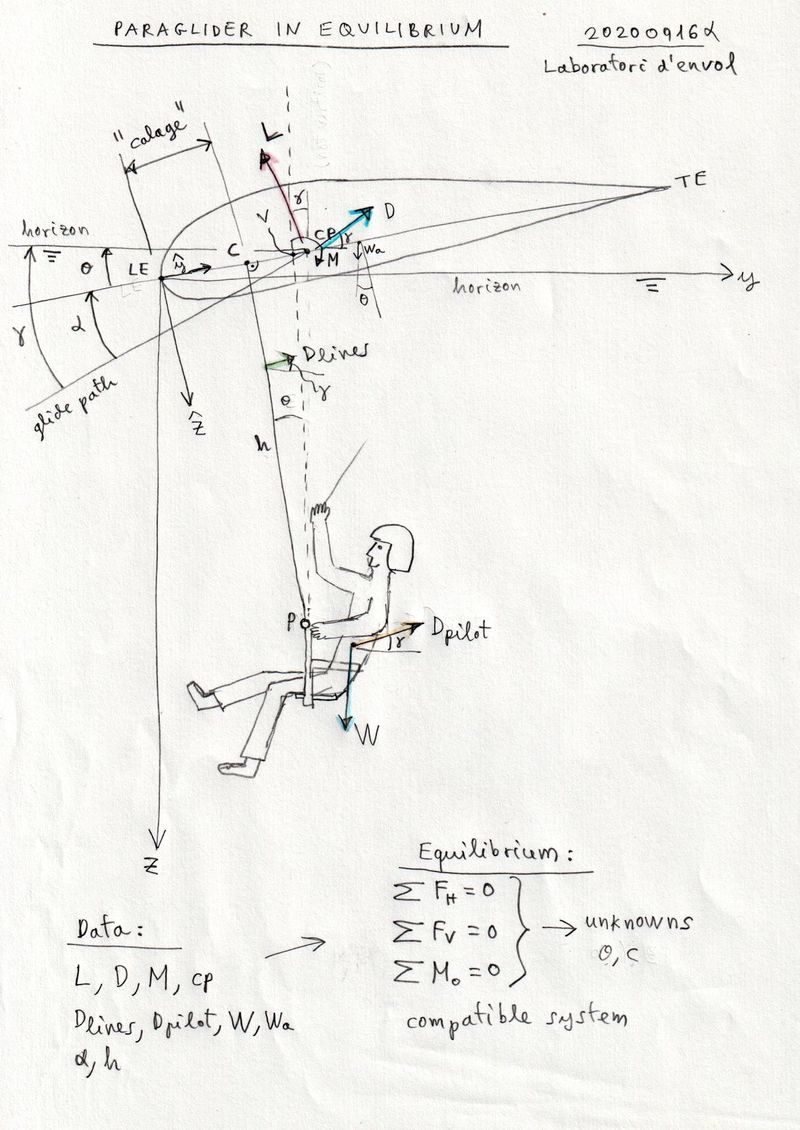
Let's imagine a simplified model of the glider. We consider a reference profile representative of the entire paraglider. And a pilot hanging below. The letter alpha represents the angle of attack, the letter gamma the glide angle, and the letter tetha the angle profile of reference with respect to the horizon. Suppose that the system is a two-dimensional rigid solid in equilibrium. Given that the system is in equilibrium, the resultant of the acting forces acting is zero. And the resultant of the moments, with respect to any point, it is also zero. But what are the forces acting on the system?
L = aerodynamic lift force, acting perpendicular to glide path
D = aerodynamic drag force, along the glide path
M = aerodynamic moment in the considered point (CP)
Wa = wing weight, acting in gravity direction
Dlines = drag of the lines, acting along the glide path
Wlines = weight og the lines, acting in gravity direction
W = weight of the pilot and harness, acting in gravity direction
Dpilot = drag of the pilot-harness acting along glide path
All of these values can be considered as "data" :) although some are not easy to determine with accuracy and representativeness.
We can also consider as a data alpha (the angle of attack of the wing) which is necessary to calculate L and D. And the height h of the pilot with respect to the wing.
And the unknowns? It seems that only the point C (calage) and the glide angle gamma. I see a lot of "data", and a few unknowns! :)
Theoretically, the system is easy to solve... Soon, we will do some tests.